TFW Ambient Monitoring Program
REPORT
FIELD COMPARISON OF
THE MCNEIL SAMPLER WITH THREE SHOVEL-BASED
METHODS USED TO SAMPLE SPAWNING SUBSTRATE
COMPOSITION IN SMALL STREAMS
Dave Schuett Hames
Bob Conrad
Allen Pleus
Devin Smith
Northwest Indian Fisheries Commission
May 1996
ACKNOWLEDGMENTS
Thanks to WFPA for funding to conduct the study.
We would like to thank the following individuals and organizations:
Thanks for the use of sampling and processing equipment to Bruce Baxter (Quinault Indian Nation); Jeff Cederholm (DNR); Jeff Dickison (Squaxin Island Tribe); Phil Peterson (Simpson Timber); Ed Salminen (Nisqually Tribe).
Thanks to Jeff Cederholm for use of the modified shovel he designed.
Thanks to Simpson Timber for access to their property on Kennedy Creek.
Thanks to the many individuals who responded to our request for information;
attended our workshop and provided feedback on the initial study results.
TABLE OF CONTENTS
The amount of fine sediments in gravel where salmonid eggs incubate is an important factor that can affect the survival of eggs and alevin (Bjornn, 1968; Phillips et al., 1975; Tagart, 1976; Cederholm et al., 1982; Tripp and Poulin, 1986; Scrivener and Brownlee, 1989; Young et al., 1990). The composition of spawning gravel, particularly the abundance of fine sediment, is often evaluated in spawning habitat assessment and monitoring projects to determine the quality of spawning habitat. The McNeil sampler (McNeil and Ahnell, 1964) was the standard equipment used to sample spawning gravel during field studies of survival to emergence in Washington State (Tagart, 1976). These data were used to establish the management indices used in the State of Washington Watershed Analysis fish habitat module (WFPB, 1995) and the McNeil sampler has been recommended as the sampling method for habitat assessment and monitoring studies collecting data in forested watersheds on state and private lands in Washington State (Schuett-Hames et al., 1994). However, the McNeil sampler has drawbacks. It is heavy and awkward to carry in the field and can be difficult to insert into large or compacted substrate. Samples are often heavy (approximately 40 lbs) and difficult to transport due to the large amount of water collected. These drawbacks have generated interest in using shovels as an alternative sampling method. Shovels are inexpensive, easy to carry, and produce lighter samples (Grost et al., 1991).
Studies comparing spawning gravel sampling methods are limited. Two systematic comparisons of spawning gravel sampling devices have been conducted, one under laboratory conditions (Young et al., 1991a) and one under field conditions (Grost et al., 1991). Ten substrate mixtures of known composition were sampled in the laboratory study, however the samples were collected from containers which did not replicate conditions encountered during field sampling in flowing streams. The McNeil sampler used in these studies did not have a plunger mechanism to retain water with suspended sediment, unlike those currently used in Washington State (Grost, personal communication). Under laboratory conditions, the McNeil sampler produced samples that most closely represented the composition of test gravel mixtures based on comparison of particles by individual size-classes and by geometric mean particle size of the entire sample. Particles greater than 50 mm were sampled inconsistently, however. The shovel produced samples similar to those of the McNeil sampler. Samples collected with single- and triple-probe freeze-cores over-sampled large particles and were likely to differ more from the actual composition of the substrate than those taken with the McNeil sampler or the shovel. The smallest size-class (particles <0.212 mm) was under-represented in samples collected by all methods. Young et al. (1991b) concluded that the McNeil sampler is the most accurate sampling device for assessing substrate composition because the variance of McNeil samples was relatively low and most frequently approximated the geometric mean particle size of the test substrates. Use of a portable stilling well was suggested to reduce the loss of sediment from shovel samples taken in flowing water (Young et al., 1991a).
The field study by Grost et al. (1991) compared groups of five paired samples from each of five sites collected with a McNeil sampler (without plunger), a shovel, and a single-probe freeze-core. The McNeil and shovel samples did not differ significantly in composition, but freeze-core samples differed from both. Shovel samples were smaller, lighter and could be taken more quickly, which made use of a shovel advantageous when sampling in remote areas (Grost et al., 1991).
The objectives of this study were to:
1) determine if the particle size composition (particularly fine sediment <0.85 mm) of samples collected with any of three shovel-based sampling methods is comparable with that of samples collected with a McNeil sampler on two stream reaches with different sampling environments;
2) compare how sample collection time and sample weight vary among sampling methods;
3) investigate the effect of water
depth, water velocity and substrate particle size on the comparability
of samples collected with the different sampling methods.
The study was designed to compare the composition of spawning gravel samples collected under field conditions using three shovel-based sampling methods to samples collected using a McNeil sampler. The three shovel-based methods examined were: (S1) a standard number 2 round-point shovel; (S2) a standard number 2 round-point shovel with a portable stilling well; and (S3) a modified shovel with side walls. To determine how various sampling methods performed under a variety of conditions, sampling was conducted in two stream reaches with different sampling environments. The study design was based on analysis of differences in composition between individual paired samples. Each paired sample consisted of a sample collected with the McNeil sampler and an adjacent sample collected with a shovel method. Based on previous data from Kennedy Creek, it was estimated that 20-30 sample pairs would be required from each stream to detect a 3 % difference in mean fine sediment between the McNeil sampler and a shovel-based method with an alpha value of 0.05 and power of 0.80. Consequently, a set consisting of 24 paired samples for each McNeil/shovel combination was collected from each stream reach. After preliminary data analysis, 14 additional sample pairs were collected to increase the power of the S2/McNeil comparison in Kennedy Creek and seven more were collected to expand the S3/McNeil comparison in Skookum Creek.
Sampling for spawning gravel composition typically occurs in channels with gradients less than 2 %, where suitable gravel is most abundant. The Watershed Analysis stream segment classification system divides stream segments within this range into two categories, those with gradients < 1 percent and those between 1 and 2 %. The first criteria for site selection was to identify a study site for each of the two gradient categories. In addition to gradient, additional site selection criteria included accessibility and a sufficient population of riffle crests suitable for sampling. Two study sites in southern Puget Sound with somewhat different channel and substrate characteristics were selected. The Kennedy Creek site was located between river kilometer 0.5 and 1.3, had a gradient of 0.45 % and a moderately confined channel. The Skookum Creek sampling site was located between kilometer 10.6 and 12.5, had a gradient of 1.4 % and an unconfined channel.
Selection of sampling locations
Samples were collected along transects across riffle crests in each stream. Riffle crests were selected as sampling locations because they are distinct, readily identifiable geomorphic features that are located at the transition between pool tailouts and riffles, two habitat areas most heavily utilized for spawning by salmonids. Working upstream through the study sites, each riffle crest was evaluated to determine its suitability for sampling by applying criteria for surface substrate particle size, water depth and velocity. To qualify for sampling, at least 1.5 m along a cross-section across the riffle crest had to be within the wetted portion of the channel, have visible water movement and be dominated by particles between 8 and 128 mm in diameter).
The distance of suitable sampling area
was measured by stretching a fiberglass tape across the riffle crest. A
random sampling procedure was used to select specific sampling locations.
If the length of suitable sampling area across the riffle crest was greater
than 4.5 m, it was divided into three equal sections and one section was
randomly chosen for sampling. If the distance was between 3 and 4.5 m,
it was divided into two sections and one was chosen. If the distance was
between 1.5 and 3 m it was not divided. The center point of the section
selected was used as the center sampling point and two additional sampling
points were located at 0.5 m from the center point in each direction along
the transect. Two paired-samples were taken at each sampling location.
The McNeil sample was always taken at the center point of the sampling
area, and one of the three shovel methods was used to collect a sample
at each adjacent sampling point. A systematic sampling strategy was used
to alternate the placement of each shovel method relative to the McNeil
sample to avoid sampling bias.
The sampling devices and procedures for collecting samples are described below.
The McNeil sampler (Mc)
The McNeil sampler was constructed of stainless steel in a standard design (Schuett-Hames et al., 1994). It consists of a round collection cylinder with a handle on top and a smaller (15 cm diameter by 23 cm long) coring cylinder attached to the bottom. Samples were collected while facing upstream. First, the coring cylinder was placed on the surface of the stream bed. Then the handle was rotated back and forth while pressing down, until the coring cylinder was fully inserted (the bottom of the collection basin was within 1.5 cm of the stream bed). Next, material in the coring cylinder was removed by hand and placed in the side of the collection basin. A plunger with neoprene seal and flapper valve was inserted into the coring cylinder to retain water and suspended sediment in the sample. After the plunger was in place, the sampler was lifted from the stream bed. Then the sample was poured into a 5 gallon plastic bucket and particles remaining inside the sampler were rinsed into the bucket.
The standard number 2 round-point shovel (S1)
The standard No. 2 round-point shovel had a wooden handle and a metal blade that was 23 cm long and 21 cm wide. Samples were collected facing upstream. The blade was held in a vertical position perpendicular to the stream bed and worked straight down into the gravel by applying pressure on the footplate while moving the handle from side to side. After the blade was fully inserted (the footplate was flush with the top of the stream bed), the shovel was pulled straight back until the blade was parallel to the stream bed surface. This procedure often required a pull/push motion to maintain the pivot point in the gravel at the junction of the footplate and the handle. Finally, the handle was grasped near the blade and the shovel was carefully removed from the stream bed while maintaining a horizontal position to avoid spilling material. The sample was placed in a clean plastic bucket and particles remaining on the blade were rinsed into the bucket.
The standard number 2 round-point shovel with portable stilling well (S2)
This treatment used the same shovel and procedure as method S1, except that a portable stilling well was placed around the shovel after it had been inserted into the stream bed. The stilling well was fabricated using four 0.64 cm (1/4 inch) sheets of aluminum that folded into a compact unit for transport. The stilling well was placed around the inserted shovel with the bow facing into the flow and the back gates adjusted to allow the handle to be lowered during removal of the sample from the stream bed. The stilling well was worked into the surface of the gravel to reduce leakage around the base.
The modified shovel (S3)
The modified shovel was designed by C. J. Cederholm (Washington Department of Natural Resources). The blade consisted of a piece of 0.32 cm (1/8 inch) steel plating measuring 33 cm long and 22 cm wide. The flat blade had short side walls designed to prevent material from sliding off the blade as samples are lifted through the water column. The sampling procedure was the same as for method S1.
Sample rejection protocol
A rejection protocol was applied to
the sampling procedures to maintain consistency. The three main criteria
used to reject samples were improper angle of insertion, incomplete insertion,
or extensive disturbance of the substrate. Rejection due to improper angle
of insertion occurred when the McNeil sampler or the shovel could not be
inserted perpendicular to the stream bed, or when the shovel blade rotated
more than 45 degrees from its initial position perpendicular to the direction
of flow. Rejection for incomplete insertion occurred when the base of the
collection basin on the McNeil sampler did not come within 1.5 cm of the
stream bed or when the shovel footplate could not be inserted flush with
the stream bed surface. Rejection due to disturbance was a subjective call
invoked when extensive mixing or disruption of the substrate occurred during
sampling because of difficulty inserting the sampling device into the stream
bed.
Measurement of water depth, water velocity, sample weight and collection time
Water depth and velocity were recorded
at each sampling location using a Swoffer flow meter with a top setting
staff. The weight of each sample (including bucket and lid) was measured
using a digital scale and recorded to the nearest 0.1 pound. A tracking
slip was placed into the bucket to help identify the sample and the bucket
was sealed. The time required to collect each sample was recorded beginning
when the sampler first made contact with the gravel and ending when the
sample was placed into the bucket and the equipment was rinsed.
Sample processing was done volumetrically
with standard equipment and methods (Schuett-Hames et al., 1994). Samples
were washed through ten sieves with openings (in mm) of 75.0, 25.0, 9.5,
3.35, 2.0, 1.0, 0.85, 0.50, 0.25, and 0.106. Wash water (including particles
washed through the 0.106 mm sieve) was collected in a catch basin and allowed
to sit for 20 minutes after the last sieve was removed. Particles settling
out during this period were collected in a graduated cylinder attached
to the bottom of the catch basin. The cylinder was removed and material
was allowed to settle for an additional 60 minutes before a volume reading
was made. Sieves were allowed to drain for 15 minutes. The volume of each
sieve was measured by placing the contents in a displacement flask and
recording the volume of displaced water that drained into a graduated cylinder.
The time required to process each sample was recorded beginning when the
sample was poured into the top sieve and ending when the volume of the
last sieve was recorded. Processing time did not include settling time
for particles < 0.106 mm.
Data Analysis and Interpretation
Comparison of substrate particle size composition
Several parameters were used to analyze substrate composition data. We compared the percentage of the total volume of material for each individual sieve size category in order to determine how methods compared over a range of size classes. We also examined the percentage of the total volume in each of three pooled size categories (>3.35 mm; 0.85 -2.00 mm; and percent fine sediment < 0.85 mm). Geometric mean particle size (GMPS), a measurement of the central tendency of the overall composition of the sample calculated by the method of moments (Young et al., 1991b) was also compared. Due to the variation observed between the study sites, data for each stream segment was analyzed separately.
To make these comparisons, first the difference between the two samples in each individual sample pair was calculated for each parameter. Then the paired-sample Wilcoxon signed-rank test (Conover, 1980) was used to compare each set of paired sample data for the McNeil sampler and each of the shovel-based methods following procedures similar to those used by Grost et al. (1991) and Young et al. (1991a). This is a nonparametric test based on the ranks of the differences between paired-samples. It does not require the assumption that the differences between pairs are identically distributed, normal random variables as does the analogous parametric procedure, the paired-sample t test (Conover, 1980). Since measurement units for the size category data used in these comparisons are percentages, and thereby constrained between 0.0 and 1.0, the data may not be normally distributed. The Wilcoxon test is also more robust to outliers than the paired-sample t test. The individual sieve size category data were compared simultaneously. To maintain an alpha level of 0.05 across all sieve size categories, the Bonferroni procedure was used (Grost et al., 1991; Young et al., 1991a). An alpha level of 0.05 was used to make comparisons between paired sample data for the pooled size categories and GMPS.
A power analysis (Peterman, 1990) was conducted to determine how large a difference between the two methods would be detected with reasonable power (i.e., power 0.80). The power of a test is the probability of rejecting the null hypothesis when it is, in fact, false and should be rejected. Power is defined as 1-b. For any hypothesis test, we want a test with a low a level (e.g., 0.05) and high power (e.g., 0.80). The methods and tables in Cohen (1988) were used to determine the power of the paired-sample Wilcoxon signed-rank test to detect differences in the mean percent fine sediment between McNeil and shovel-based samples.
Effects of water depth, water velocity and substrate size on the percentage of fine sediment
To identify physical stream channel characteristics influencing the comparability of shovel samples with McNeil samples, we examined the relationships between differences in the percentage of fine sediment (particles <0.85 mm) between paired samples, and variables such as water depth, water velocity, and several parameters used to characterize substrate conditions (e.g., abundance of large particles that make sample collection difficult). Both Pearson's parametric correlation coefficient (r) and Spearman's nonparametric (Conover, 1980) correlation coefficient () were used. Ordinary least-squares (OLS) linear regression was used to examine functional relationships between some of the parameters measured (Kleinbaum and Kupper, 1978).
Comparison of mean sample weight and time required to collect samples
Data on sample weight and collection time were examined to determine if collecting samples with shovel-based methods would increase sampling efficiency in the field. Analysis of variance (ANOVA) or the Kruskal-Wallis (KW) test were used to compare differences in these parameters among sampling methods. ANOVA tests require that all groups come from normally-distributed populations with equal variances (homogenous variance assumption). While most ANOVA procedures are robust to departures from normality they can be sensitive to violations of the homogeneous variance assumption (Milliken and Johnson, 1992). Levene's test for homogeneity of variances (Milliken and Johnson, 1992) was used to test for this assumption. When the hypothesis of homogeneous group variances was rejected the nonparametric equivalent of the ANOVA, the KW test(Conover, 1980), was used to examine the data for between-group differences. Two necessary assumptions for the KW test are: (1) the data are random samples from their respective populations; and (2) there is mutual independence among the groups. When either the ANOVA or KW test was significant (P 0.05), indicating between-group differences, pair-wise multiple-comparison tests were used to determine which groups were different.
Three topics are addressed in this
section: 1) comparison of substrate particle size composition of samples
collected with the McNeil sampler to those taken with shovel-based sampling
methods; 2) comparison of the effect of water depth, water velocity,
and substrate size on the substrate composition of samples from different
sampling methods, and 3) comparison of measures of sampling efficiency
such as sample weight and collection time for
different sampling methods.
Comparison of Substrate Particle Size Composition
The following section compares differences in the substrate particle size composition of samples collected with the McNeil sampler and each of the three shovel-based sampling methods. Overall substrate composition was compared by examining the percentage of total volume in each sieve size category. In addition, two parameters related to salmon survival to emergence were examined, the percentage of fine sediment <0.85 mm (%Fines) and geometric mean particle size (GMPS). Results for each stream reach are treated separately because our analysis indicated there were significant differences between them.
Comparison by particle size category
The Wilcoxon signed-rank test was used to compare sample size-fractions for each sieve size in order to determine if the shovel-based samples were comparable with McNeil samples across size classes and to identify which size classes were responsible for differences in methods. The largest sieve size (75 mm) was omitted from the tests comparing sample size-fractions in Kennedy Creek because they occurred in only four of 136 samples from Kennedy Creek. The volume of particles of this size were included in the overall total volume used to calculate percent volume for the other sieve sizes, however. The comparison at the largest sieve size (75 mm) was included in the overall test for Skookum Creek since particles of this size occurred in 32 (26 %) of the samples.
The results of the Wilcoxon tests for Kennedy Creek are summarized in Table 1. More detailed comparisons of each shovel-based method to the McNeil sampler are given in Appendix Table 1 (McNeil to S1), Appendix Table 2 (McNeil to S2), and Appendix Table 3 (McNeil to S3). Because only ten sieve sizes were used for the overall comparison, the alpha level to determine the significance of the individual tests was 0.005 (0.05 overall alpha divided by 10 tests). There was a significant (P 0.005) difference between samples from all three shovel-based methods and McNeil samples for at least one size category in Kennedy Creek. The proportional volume of material in the smallest size category (<0.106 mm) was significantly different between the McNeil samples and the samples from all three shovel-based methods. Under the Bonferroni conditions, we concluded that the overall particle size composition of samples from Kennedy Creek collected with each of the shovel-based methods was significantly different from the composition of samples obtained with the McNeil sampler.
The results of the Wilcoxon tests for Skookum Creek are also summarized in Table 1. More detailed comparisons of each shovel-based method to the McNeil sampler are given in Appendix Table 4 (McNeil to S1), Appendix Table 5 (McNeil to S2), and Appendix Table 6 (McNeil to S3). Because 11 sieve sizes were used to characterize the overall comparison, the alpha level to determine the significance of the individual tests was 0.00455 (0.05 overall alpha divided by 11 tests). The S1 and S2 methods each had at least one sieve size with a significant (P 0.00455) difference from the McNeil sampler. The proportional volume of material in the smallest size category (< 0.106 mm) was significantly different between the McNeil samples and the samples for both of these methods in Skookum Creek. Under the Bonferroni conditions, we concluded that the overall particle size composition of samples from Skookum Creek obtained using the S1 and S2 methods was significantly different from the composition of samples taken with the McNeil sampler. There was not a significant difference in particle size composition between samples collected with the S3 method and the McNeil method.
Table 1. Significance levelsa of the paired-sample Wilcoxon signed-rank tests for comparing the McNeil sampler to the three shovel-based methods.
| Parameter | McNeil to S1 | McNeil to S2 | McNeil to S3 | |||
| Kennedy | Skookum | Kennedy | Skookum | Kennedy | Skookum | |
| Sieve size category | ||||||
| 75.00 mm | 0.012 | 0.164 | 0.358 | |||
| 25.00 mm | 0.603 | 0.320 | 0.279 | 0.452 | 0.331 | 0.349 |
| 9.50 mm | 0.584 | 0.208 | 0.184 | 0.006 | 0.418 | 0.080 |
| 3.35 mm | 0.663 | 0.023 | 0.040 | 0.079 | 0.293 | 0.034 |
| 2.00 mm | 0.638 | 0.003 | 0.323 | 0.241 | 0.983 | 0.238 |
| 1.00 mm | 0.390 | 0.473 | 0.912 | 0.922 | 0.648 | 0.256 |
| 0.85 mm | 0.088 | 0.589 | 0.227 | 0.478 | 0.550 | 0.632 |
| 0.50 mm | 0.033 | 0.317 | 0.074 | 0.331 | 0.763 | 0.950 |
| 0.25 mm | 0.966 | 0.267 | 0.275 | 0.119 | 0.027 | 0.067 |
| 0.106 mm | 0.099 | 0.226 | 0.337 | 0.052 | 0.000 | 0.027 |
| <0.106 mm | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.035 |
| Pooled Categories | ||||||
| 3.35 mm | 0.005 | 0.541 | 0.464 | 0.944 | 0.002 | 0.977 |
| 0.85-2.00 mm | 0.452 | 0.089 | 0.509 | 0.877 | 0.877 | 0.211 |
| % Fines (< 0.850 mm) | 0.001 | 0.546 | 0.302 | 0.570 | 0.000 | 0.533 |
| GMPS | 0.030 | 0.197 | 0.819 | 0.422 | 0.023 | 0.308 |
Both the S1 and S2 shovel-based methods had significant differences in at least one particles size class in both Kennedy and Skookum Creek. The S3 shovel method had significant differences in two particle size classes in Kennedy Creek but no significant differences in Skookum Creek. All of the seven cases where significant differences occurred between a shovel-based method and the McNeil sampler involved particles < 3.35 mm in diameter, and five of seven cases involved the smallest particle size category (particles < 0.106 mm). In all five cases where a significant difference was detected (as well as in the case where the difference was not significant), the McNeil samples contained a greater mean percentage of material <0.106 than the shovel-based methods (Appendix Tables 1-6). We suspect this is because the plunger of the McNeil sampler captures water containing suspended sediment in the sample. Consequently, it appears that a limitation of shovel-based methods is their failure to capture fine sediment that becomes suspended when the substrate is disturbed during sampling.
Comparison by percent fine sediment
A major focus of this study was to determine the comparability of the percentage of fine sediments in samples collected by shovel-based methods with McNeil samples. For the purposes of this study, fine sediments were defined as particles <0.85 mm in diameter (%Fines). The percentage of fine sediments in salmonid spawning gravel has been correlated with the survival to emergence (Cederholm et al., 1982), and to human management activities (Young et al., 1991b). In addition, the percentage of fine sediment < 0.85 mm is used as a management indicator of spawning gravel quality in the Watershed Analysis procedure used by Washington State to evaluate cumulative effects on forest lands (WFPB, 1995).
Limiting the comparison to the %Fines category for Kennedy Creek samples, there was not a significant difference between McNeil and S2 samples (Table 1). The mean difference in %Fines between S2 samples and McNeil samples was + 1.0 % (Appendix Table 2). In the McNeil/S2 comparison, McNeil samples had greater %Fines than shovel samples in 58 % (22 of 38) of the pairs (Appendix Table 2). The hypothesis that %Fines for the McNeil and S2 samples from Kennedy Creek were equal could not be rejected (P = 0.302). The S1 and S3 samples were significantly different (P 0.001) from the McNeil samples in Kennedy Creek. The mean difference in %Fines between S1 and S3 samples and McNeil samples was +2.9 % and +4.7 %, respectively (Appendix Tables 1 and 3). McNeil samples had greater %Fines than the paired shovel samples for the majority of S1 (83 %) and S3 (79 %) comparisons (Figure 1). Using methods and tables in Cohen (1988), the power of the test to detect a 2 % difference in mean percent fines between the McNeil sampler and the S2 method was estimated to be about 0.62. The power of the test to detect a 3 % difference in mean %Fines was estimated to be about 0.93. The observed difference in mean %Fines was 1.0 %. We conclude that the test had adequate power (> 0.80) to detect differences as large as those observed between the S1 method and McNeil sampler (2.9 %) and the S3 method and McNeil sampler (4.7 %). We cannot conclude that a mean difference of 2.0 % or less for the S2/McNeil comparison would have been detected with adequate power.
For Skookum Creek samples, there was not a significant difference (all P > 0.50) in the %Fines category between any shovel-based methods and the McNeil sampler (Table 1). The mean difference in %Fines between the S1, S2, and S3 samples and McNeil samples was -1.1 %,
-0.6 % and -1.4 %, respectively (Appendix Tables 4, 5, and 6). The %Fines for McNeil samples was greater than shovel-based samples about half the time (Figure 1). The McNeil value for %Fines was greater in 50 % of sample pairs for the McNeil/S1 comparisons, 42 % of sample pairs for the McNeil/S2 comparisons, and 48 % of sample pairs for the McNeil/S3 comparisons.

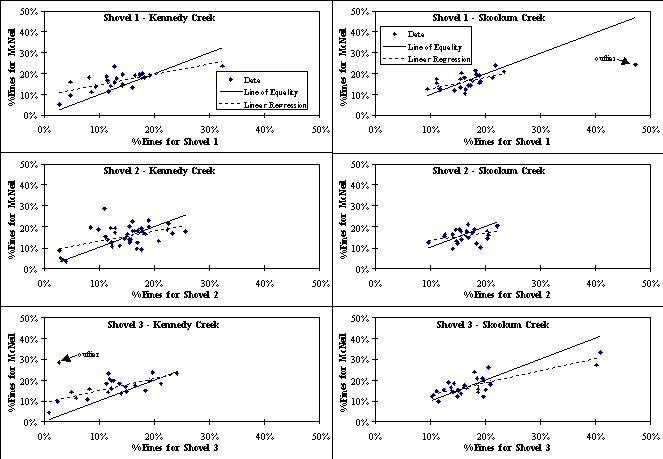
Figure 1. Comparison of the proportion of fine sediment
(<0.85 mm) in paired shovel-based samples (x-axis) and McNeil samples
(y-axis) from Kennedy and Skookum Creeks.
The hypothesis that %Fines for the McNeil and shovel-based samples from Skookum Creek were equal could not be rejected for any of the shovel-based methods (all P > 0.50). A power analysis was conducted to determine how large a difference between the McNeil and each shovel-based method would be detected with reasonable power (i.e., power 0.80). The power of the test comparing the McNeil to the S1 method to detect a 2 % difference in mean percent fines was estimated to be about 0.49. The power of the test to detect a 3 % difference in mean %Fines was estimated to be about 0.81. The observed difference in mean %Fines was 1.1 %. For the McNeil/S2 comparison, the power to detect a 2 % difference was 0.75 and the power to detect a 3 % difference was 0.97. The observed difference in mean %Fines for the McNeil/S2 comparison was 0.6 %. For the McNeil/S3 comparison, the power to detect a 2 % difference was 0.54 and the power to detect a 3 % difference was 0.87. The observed difference in mean %Fines for the McNeil/S3 comparison was 1.4 %. We conclude that the tests had adequate power (> 0.80) to detect differences of 3 % or greater. We cannot conclude that mean differences of 2.0 % or less would have been detected with adequate power.
OLS linear regression was used to examine the relationship between %Fines for the McNeil samples and each of the shovel-based methods and to determine if a regression could be used to convert the mean %Fines for shovel-based samples into the McNeil sampler equivalent. For Kennedy Creek there was a significant linear relationship between %Fines for each shovel-based method and the McNeil samples. A single point was identified as an outlier for the S3/McNeil relationship (Figure 1). There is considerable scatter of the data around these regression lines (Figure 1) and the proportion of total variation about the mean explained by the regressions (R2) was low for all three relationships. R2 values were 0.48, 0.38, and 0.51 for the S1, S2, and S3 methods, respectively. Only in the case of the S3 method was more than 50 % of the variation around the mean explained by the regression. Because of the large amount of variation, these regression lines are not useful for converting shovel-based measurements to equivalent McNeil measurements for %Fines. The distributions of the data around each line of equality in Figure 1 illustrate the bias of the S1 and S3 methods. For both of these methods, the majority of the data are above the line of equality indicating that the S1 and S3 methods generally underestimate the %Fines compared to the McNeil sampler in Kennedy Creek. The S2 method appears unbiased as the data are about equally distributed above and below the line of equality.
For Skookum Creek, there was a significant (P < 0.05) linear relationship between the %Fines for the S1 and S3 shovel methods and the McNeil samples. However, the hypothesis of zero slope could not be rejected for the S2 versus McNeil relationship (P = 0.098). There was a single point identified as an outlier for the S1 versus McNeil relationship (see Figure 1). The proportion of the total variation about the mean explained by the regressions was low for all three relationships. R2 values were 0.34, 0.12, and 0.54 for the S1, S2, and S3 methods, respectively. Only in the case of the S3 method was more than 50 % of the variation around the mean explained by the regression. There is considerable scatter of data around the regression lines (Figure 1), as in the Kennedy Creek data, and it is doubtful the regressions would be useful for converting the shovel-based measurements to equivalent McNeil measurements.
The distributions of data around each line of equality in Figure 1 illustrates that the bias present in the S1 and S3 methods for the Kennedy Creek samples was not present in the Skookum Creek samples. For all three shovel-based methods the data are about equally distributed above and below the lines of equality.
Comparison by geometric mean particle size
Geometric mean particle size (GMPS) is a measure of spawning gravel composition that characterizes the central tendency of the particle size distribution of the entire sample. GMPS was determined to be the most sensitive indicator of cutthroat trout survival to emergence in an earlier study (Young et al., 1991b).
The results of the comparison of GMPS between sampling methods for Kennedy Creek were similar to those for %Fines. The GMPS for the S1 and S3 samples were significantly different (P 0.05) from the McNeil samples while the S2/McNeil comparison was not significantly (P = 0.819) different (Table 1). For Skookum Creek, there was not a significant difference (all P > 0.19) between any of the shovel-based samples and McNeil samples (Table 1).
OLS linear regression was used to examine the relationship between GMPS for McNeil samples and each of the shovel-based methods. For Kennedy Creek, there was a significant (P < 0.01) linear relationship between GMPS for each shovel-based method and the McNeil sampler. R2 values were 0.32, 0.66, and 0.56 for the S1, S2, and S3 methods, respectively. For both the S2 and S3 methods more than 50 % of the variation around the mean was explained by the regression. For Skookum Creek, there was a significant (P < 0.01) linear relationship between GMPS for the S1 and S3 methods and the McNeil samples. However the hypothesis of zero slope could not be rejected for the S2/McNeil relationship (P = 0.126). The proportion of the total variation about the mean explained by the regressions was low for all three relationships. R2 values were 0.40, 0.10, and 0.31 for the S1, S2, and S3 methods, respectively. There is considerable scatter of data around the regression lines for both the Kennedy and Skookum Creek data (Figure 2). Because of the large amount of variation, these regression lines are not useful for converting shovel-based measurements to equivalent McNeil measurements for GMPS.
The distributions of data around each line of equality
in Figure 2 illustrate the bias of the S1 and S3 methods in Kennedy Creek.
For both of these methods, the majority of the data are below the line
of equality. For the S1 comparison, the shovel-based measurement of GMPS
was greater than the McNeil measurement of GMPS in 67 % of the pairs. For
the S3 comparison, the shovel-based measurement of GMPS is greater than
the McNeil measurement of GMPS in 71 % of the pairs. Therefore, these methods
generally overestimate GMPS compared to the McNeil sampler. The S2 method
appears unbiased as the data are about equally distributed above and below
the line of equality (53 % of the pairs are below the line and 47 % are
above). The distributions of data around each line of equality in Figure
2 can also be used to assess the bias of the methods in Skookum Creek.
For the S1 method, the majority of the data (63 % of the data pairs) are
below the line of equality. Therefore, the S1 method generally overestimated
GMPS compared to the McNeil sampler for Skookum Creek. For the S2 comparison,
the shovel-based measurement of GMPS is greater than the McNeil measurement
of GMPS in 58 % of the data pairs. The data are about equally distributed
above and below the line of equality for the S3 method (the GMPS of shovel-based
samples was greater than that of McNeil samples in 52 % of the data pairs).
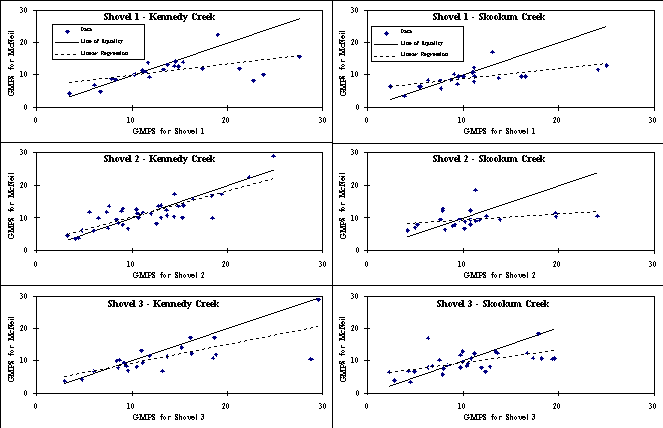
Figure 2. Comparison of geometric mean particle size (GMPS)
in paired shovel-based samples (x-axis) the McNeil samples (y-axis) from
Kennedy and Skookum Creeks.
Discussion of the substrate particle size composition analysis
The McNeil sampler was defined as the standard against which the shovel-based methods were compared in this study. This implies that particle size composition estimated from McNeil samples more accurately reflects the actual composition of the stream bed (Young et al., 1991a). The three shovel-based methods can be adequate substitutes for the McNeil sampler if either:
1. The estimates of important particle size composition parameters from shovel-based samples are unbiased, not significantly different , and of similar precision to estimates from McNeil samples,
OR
2. The estimates of important particle size composition parameters from shovel-based samples have a consistent relationship with estimates from McNeil samples and the form of the relationship can be statistically described. This relationship can then be used to convert a shovel-based estimate to its corresponding McNeil sample equivalent, however, the relationship must be able to provide "corrected" estimates of similar precision to the estimates from the McNeil sample.
For the individual sieve category data, there was a significant difference (overall P < 0.005) between the estimated proportional contribution to the total sample volume of at least one sieve size for five of the six McNeil-to-shovel comparisons evaluated. The proportion of the smallest particle size category (< 0.106 mm) was significantly different between the McNeil and the shovel-based methods in all five of the significant comparisons. The only comparison for which there were no significant differences across all sieve sizes was the McNeil/S3 comparison at Skookum Creek.
For %Fines (particles < 0.850 mm) however, only two of six McNeil-to-shovel comparisons evaluated were significantly different (the McNeil-to-S1 and McNeil/S3 comparisons at Kennedy Creek). It is interesting to note that the direction of the mean differences between the McNeil and the shovel-based methods was different between the two sampling locations. In Kennedy Creek, mean %Fines was less for samples from the three shovel-based methods than the paired McNeil samples, while in Skookum Creek mean %Fines was greater for samples from the three shovel-based methods than the paired McNeil samples (Table 2; Figure 3).
Table 2. Summary statistics for the mean difference in %Fines between each shovel-based method and the McNeil sampler for samples collected at Kennedy and Skookum Creeks.
| Shovel/McNeil | Mean % | Standard | Coefficient | Min. % | Max. % | |||
| Comparison | Difference | Error | of Variation | 95% Conf. Interval | Difference | Difference | ||
| Kennedy Cr. | ||||||||
| Shovel 1 | 2.9% | 0.9% | 30.9% | 1.0% | - | 4.7% | -8.9% | 11.2% |
| Shovel 2 | 1.0% | 0.9% | 85.1% | -0.7% | - | 2.8% | -8.2% | 17.5% |
| Shovel 3 | 4.7% | 1.2% | 25.8% | 2.2% | - | 7.2% | -3.6% | 25.8% |
| Skookum Cr. | ||||||||
| Shovel 1 | -1.1% | 1.2% | 105.5% | -3.5% | - | 1.3% | -23.3% | 6.2% |
| Shovel 2 | -0.7% | 0.7% | 113.8% | -2.2% | - | 0.9% | -8.8% | 4.4% |
| Shovel 3 | -1.4% | 1.1% | 80.7% | -3.7% | - | 0.9% | -26.9% | 5.9% |
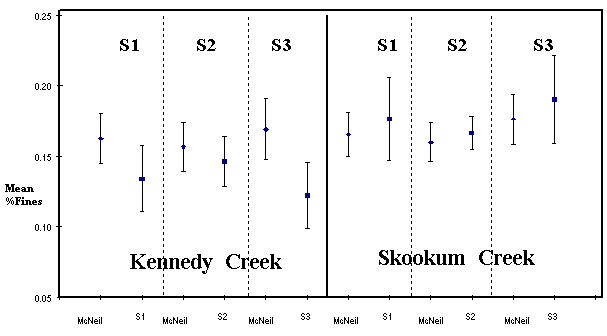
Figure 3. Comparison of mean %Fines (and 95 % confidence
intervals) for the McNeil samples and the paired shovel-based samples collected
at Kennedy and Skookum Creeks.
Only the S2 method produced samples that were not significantly different from the paired McNeil samples in percent fine sediments at both locations (Mann-Whitney test, P = 0.23). The mean difference in percent fine sediment between the S2 samples and the paired McNeil samples was +1.0 % at Kennedy Creek and -0.7 % at Skookum Creek (Table 3). Bias between the S2 and McNeil samples was not evident at either location (Figure 1). The precision (coefficient of variation) of the shovel-based samples varied relative to that of the paired McNeil samples (Table 3). Shovel method S2 exhibited similar or better precision than the McNeil sampler while methods S1 and S3 were less precise.
Table 3. Comparison of sample sizes, mean percent fine sediment (mean %Fines), standard error, and coefficient of variation for the McNeil and each shovel treatment by stream.
| Mc | S1 | Mc | S2 | Mc | S3 | |
| Kennedy Creek | ||||||
| Sample Size | 24 | 24 | 38 | 38 | 24 | 24 |
| Mean %Fines | 16.3 % | 13.4 % | 15.7 % | 14.7 % | 16.9 % | 12.2 % |
| Standard Error | 0.0087 | 0.0123 | 0.0087 | 0.0088 | 0.0105 | 0.0124 |
| Coeff. of Var. | 5.4% | 9.2% | 5.6 % | 6.0 % | 6.2 % | 10.2 % |
| Skookum Creek | ||||||
| Sample Size | 24 | 24 | 24 | 24 | 31 | 31 |
| Mean %Fines | 16.5 % | 17.7 % | 16.0 % | 16.7 % | 17.7 % | 19.0 % |
| Standard Error | 0.0078 | 0.0147 | 0.0065 | 0.0064 | 0.0091 | 0.0163 |
| Coeff. of Var. | 4.7% | 8.3% | 4.1 % | 3.8 % | 5.2 % | 8.6 % |
Table 4. Comparison of ability of three
shovel-based sampling methods to meet the criteria for substitution for
the McNeil sampler.
| Sampler | Test 1a - Unbiased | Test 1b -
Not significantly different |
Test 1c -
Similar Precision |
Test 2-
Consistent correctable relationship |
||||
| Kennedy | Skookum | Kennedy | Skookum | Kennedy | Skookum | Kennedy | Skookum | |
| S1 | no | yes | no | yes | no | no | no | no |
| S2 | yes | yes | yes | yes | yes | yes | no | no |
| S3 | no | yes | no | yes | no | no | no | no |
Consequently, it appears that the standard shovel with
stilling well (S2) can be an adequate substitute for the McNeil sampler
for determining the percentage of fine sediment < 0.85 mm in stream
channels similar to those we sampled. This conclusion was drawn because
S2 samples met the first set of conditions for an adequate substitute:
no significant difference was detected in average percent fine sediments
between S2 samples and McNeil samples; the percentage of fine sediments
in S2 samples did not appear biased (either high or low) in comparison
with McNeil samples; and S2 samples had similar precision to McNeil samples.
Since only two stream reaches were sampled, it is unknown if the S2 method
would produce comparable samples in other situations. Recommendations for
application of the S2 sampling method to monitoring studies are presented
in the recommendations section at the end of this report.
Effects of Water Depth, Water Velocity, and Substrate Size on Percentage of Fine Sediment
This portion of the study was designed to determine whether differences in the percentage of fine sediments between samples collected with the McNeil sampler and the shovel-based methods could be explained by conditions at the sample site such as water depth, velocity or substrate size.
Water depth and water velocity
The average water velocity at the Kennedy Creek sampling sites was 0.31 m/sec, or about 0.09 m/sec faster than at the Skookum Creek sample sites. The average water depth of the samples collected from Kennedy Creek was 0.1 m, about 0.04 m deeper than the samples collected from Skookum Creek. If these parameters affect the gravel sampling methods, this may explain the differences observed between the streams for %Fines as measured by the McNeil samples in comparison to the three shovel-based methods. For example, the difference in %Fines between a McNeil and a shovel-based sample might increase as the water velocity or depth increases.
There were only two significant correlations among the 48 relationships examined between water depth or velocity and the difference in %Fines between McNeil samples and the shovel-based samples (Table 5). The Pearson's correlation coefficients between the depths of the McNeil and S2 shovel samples and the difference in %Fines were significant (P 0.01) at Kennedy Creek.
Table 5. Summary of Pearson's (r) and Spearman's () correlation coefficients between specified parameters and the difference in %Fines between paired McNeil and shovel samples collected from Kennedy (K) and Skookum (S) Creeks.
| S1 | S2 | S3 | ||||||||||
| Parametera | rb | r | r | |||||||||
| K. | S. | K. | S. | K. | S. | K. | S. | K. | S. | K. | S. | |
| McNeil Depth | 0.450 | 0.080 | 0.380 | -0.018 | 0.449 | -0.342 | 0.388 | -0.354 | 0.502 | 0.191 | 0.310 | 0.186 |
| Shovel Depth | 0.509 | 0.105 | 0.437 | 0.174 | 0.431 | -0.154 | 0.345 | -0.146 | 0.396 | 0.218 | 0.173 | 0.193 |
| McNeil Velocity | 0.060 | -0.197 | 0.083 | -0.221 | 0.356 | -0.501 | 0.387 | -0.400 | 0.174 | -0.045 | 0.028 | 0.078 |
| Shovel Velocity | 0.429 | 0.032 | 0.483 | 0.144 | 0.113 | -0.263 | 0.175 | -0.180 | 0.146 | -0.089 | -0.055 | -0.090 |
| McNeil Time | -0.068 | -0.061 | -0.015 | -0.250 | 0.296 | -0.020 | 0.179 | -0.066 | 0.522 | -0.092 | 0.332 | -0.232 |
| Shovel Time | 0.337 | 0.531 | 0.390 | 0.526 | 0.364 | 0.522 | 0.331 | 0.448 | 0.406 | 0.291 | 0.426 | 0.251 |
| McNeil Large | 0.379 | 0.117 | 0.385 | -0.008 | 0.058 | 0.041 | 0.070 | 0.057 | 0.156 | 0.176 | 0.216 | 0.040 |
| Shovel Large | 0.731 | 0.763 | 0.730 | 0.603 | 0.545 | 0.792 | 0.551 | 0.803 | 0.623 | 0.732 | 0.673 | 0.529 |
| McNeil Inter | -0.470 | -0.046 | -0.461 | -0.106 | -0.379 | -0.373 | -0.433 | -0.116 | -0.420 | -0.002 | -0.356 | -0.134 |
| Shovel Inter. | -0.542 | -0.290 | -0.569 | -0.288 | -0.460 | -0.716 | -0.475 | -0.688 | -0.474 | -0.164 | -0.418 | -0.297 |
| McNeil GMPS | 0.279 | 0.152 | 0.281 | 0.104 | 0.132 | -0.054 | 0.190 | 0.029 | 0.108 | 0.088 | 0.255 | 0.043 |
| Shovel GMPS | 0.685 | 0.509 | 0.730 | 0.499 | 0.439 | 0.656 | 0.512 | 0.660 | 0.636 | 0.575 | 0.555 | 0.589 |
b Correlation's which are significant at P
0.01 are indicated by bold type.
The general lack of significant correlations indicates that neither depth of sample or water velocity alone can explain the direction (positive or negative) of the differences between the McNeil and shovel-based methods at the two sample locations. Appendix Figures 1 and 2 show the relationships between water depth and water velocity, respectively, and the difference in %Fines for each shovel-based method and stream combination. The method (McNeil or Shovel) with the highest correlation is shown in these figures. No clear linear trends are evident.
We next examined whether using water depth and velocity
at the sampling site could improve the predictive ability of the regressions
between the %Fines for a shovel-based method and the McNeil sampler. The
R2 values for the regressions between %Fines for shovel-based
samples and McNeil samples ranged from 0.38 to 0.51 for Kennedy Creek and
between 0.12 and 0.54 for Skookum Creek (Figure 1). Stepwise linear regression
(Draper and Smith 1981) was used to determine if adding water depth or
water velocity to the regression model would significantly improve these
relationships. An F-to-enter criteria of 0.05 was used for adding one of
these parameters to the regression model. For none of the six regression
models (one for each of three shovel-based methods at each sample location),
did the addition of either water depth or water velocity to the model significantly
improve the relationship (i.e., significantly increase the proportion of
the total variation about the mean ![]() explained by the regression).
explained by the regression).
Neither water depth nor water velocity at the sample site sufficiently explain why the relationship between the difference in %Fines between McNeil samples and shovel-based samples is in different directions for Kennedy Creek (%Fines for the McNeil sample usually higher than the paired shovel sample) and Skookum Creek (%Fines for the McNeil sample usually lower than the paired shovel sample). These parameters do not significantly improve the regressions relating %Fines for shovel-based samples to %Fines for McNeil samples.
Another factor that might influence the difference in %Fines between methods is substrate composition. For example, the difference in %Fines between a McNeil sample and a shovel-based sample might increase as substrate size increases due to differences in the performance of various samplers when large particles are encountered. Four different parameters were examined as indicators of overall substrate size. They were: large particles 3.35 mm (%Large), intermediate particles from 0.85 mm to 2.00 mm; geometric mean particle size; and sample collection time. Sample collection time was included because it was thought that longer collection times usually corresponded with the presence of large particles and increased difficulty in collecting samples.
The only parameter with significant correlation coefficients (P 0.01) across all twelve comparisons (two correlation coefficients x 3 shovel-based methods x 2 locations) was for the proportion of the sample volume with particles 3.35 mm for the shovel-based methods (%Large). This parameter had the largest correlation coefficient in nearly every comparison for the difference in %Fines and %Large, ranging from 0.529 to 0.803 (Table 5). The only comparable parameter was GMPS for the shovel-based samples which had significant correlations for 10 of the 12 comparisons (Table 5). Appendix Figure 3 shows the relationship between the difference in %Fines and the proportion of sample volume 3.35 mm (%Large) for the shovel-based samples. All six of these relationships indicate that as substrate size increases the difference in %Fines between the McNeil sampler and shovel-based methods increases.
The difference in overall substrate size may explain the
difference in mean %Fines observed between the two creeks. Larger differences
in %Fines were associated with larger overall substrate sizes. A greater
volume of the Kennedy Creek samples was composed of larger particles (mean
%Large values of 0.78, 0.75, and 0.77 for the S1, S2, and S3 methods, respectively)
than the Skookum Creek samples (mean %Large values of 0.66, 0.67, and 0.66
for the S1, S2, and S3 methods, respectively). However, Skookum Creek had
the largest percentage of samples with particles greater than 75 mm. Further
investigation of the relationship between substrate composition and differences
between %Fines between sampling methods is warranted.
Comparison of Field and Processing Efficiency of Sampling Devices
Information comparing the weight and cost of sampling devices, sample collection and processing times, and sample weight and volume for the four sampling methods is provided in Table 6. This information can be used by field managers to determine the advantages and disadvantages of various sampling devices.
Table 6. Comparison of sampler weight, cost, and mean
sample collection and processing times, carry-out weight, and volume displacement
for both streams.
| Sampler | Unit Weight
(lbs) |
Unit
Cost |
Mean Collection Time (min) | Mean Processing Time (min) | Mean Carry-out weight (lbs) | Mean Volume Displacement
(ml) |
| McNeil (Mc) | 25.3 | $350 | 9.1 | 47.6 | 43.5 | 3583 1 |
| Shovel (S1) | 3.8 | $15 | 2.3 | 45.5 | 18.4 | 2867 |
| Shovel with Stilling Well (S2) | 3.8
21.6 |
$15
$1202 |
3.1 | 46.2 | 19.4 | 3015 |
| Modified. Shovel (S3) | 8.3 | $1753 | 4.3 | 50.3 | 25.3 | 4049 |
1 A 15 cm dia. x 23 cm cylinder has a volume of 4064 cm3 or 4024 ml (3583 ml = 89% of absolute volume)
2 Reduce cost of stilling well by making it out of plywood for smaller projects
3 Cost of S3 reflects prototype cost - production
of a set design may be much cheaper
Table 6 reports average weight for samples from Kennedy and Skookum Creeks taken with each sampling method. In Kennedy Creek, there were significant among-method differences for mean sample weight (KW test, P < 0.001). Multiple comparison tests indicate that mean weights for all methods were significantly (P < 0.01) different from each other. McNeil samples were heaviest and samples from the S1 method were lightest. In Skookum Creek, there were also significant among-method differences for mean sample weight (ANOVA, P < 0.001). Multiple comparison tests indicate that mean weights for S1 and S2 samples were not significantly different from each other (P > 0.05) but that all other methods were significantly different from each other (P < 0.05). As with the Kennedy Creek samples, McNeil samples were heaviest and S1 samples were lightest.
The volume of material collected by the various sampling techniques also varied (Table 6). S3 samples had the greatest average volume (4049 ml), followed by McNeil samples (3582 ml), S2 samples (3015 ml) and S1 samples (2867 ml). The volume of McNeil samples is already below that recommended to characterize coarse bed material in rivers (Church et al., 1987). A further reduction in the size of samples obtained with the standard shovel (S1 and S2) would be expected to increase sampling variability.
There were also significant among-method differences for mean time required to collect samples at both sites (KW test, P < 0.001). For Kennedy Creek, multiple comparison tests indicate mean collection times for the S2 and S3 methods were not significantly different (P > 0.05) but that all other methods were significantly (P < 0.01) different from each other (Table 6). For Skookum Creek, multiple comparison tests indicate that mean collection times for the S1 and S2 methods were not significantly different (P > 0.05) but that all other methods were significantly different from each (P < 0.01). McNeil samples had the longest mean collection time and samples from the S1 method had the shortest mean collection time for both sites (Table 6). Substantially more time was required to collect samples using the McNeil sampler than any shovel-based sampling method. It took an average of 9.1 minutes to collect a McNeil sample, while standard shovel methods (S1 and S2) required only 2.3 and 3.1 minutes, respectively, per sample on average and modified shovel (S3) samples required 4.3 minutes. Collection time was generally greater in Skookum Creek than in Kennedy Creek.
Discussion of factors affecting sampling efficiency
The collection weight of each sample includes the weight of the 5 gallon plastic bucket and the water captured during the sampling procedure and rinsing the equipment. It is best viewed as "carry-out" weight. Differences in sample weights were affected primarily by equipment design, water depth and velocity at the sample site. The average weight of samples taken with the S1 and S2 methods was only about half the average weight of McNeil samples. The greater weight of McNeil samples appears to be due in part to the volume of water captured by the plunger and additional water required to rinse particles off the inside surfaces of the sampler. The amount of water captured in the McNeil varies with water depth, and can be substantial when water is deeper than 10 cm. When water depth exceeded 20 cm, two buckets were required to hold the water from one sample and the sample collection weight was over 65 lbs. Conversely, the field crew observed that more sediment was washed off the blades of the shovels as water depth and velocity increased. Modified shovel (S3) samples were approximately six pounds heavier than those taken with the standard round-point shovel (S1 and S2). This appears to be due to the greater length and collection area of the modified shovel, and the side walls that reduced the amount of material sliding off the shovel blade as it was lifted through the water column.
The range of collection times for each treatment was influenced by equipment design, substrate armoring and composition, and the strength and body weight of the people collecting samples. Equipment design and the resulting sampling protocol was one of the most influential factors regulating sample collection time. The standard shovel (S1) was the fastest sampling tool because it was relatively easy to insert into the stream bed, and it could be quickly unloaded and rinsed. The time required to collect S2 samples averaged approximately a minute longer than S1 samples, reflecting the additional time required to set up the portable stilling well. The modified shovel (S3) had a longer mean collection time than the standard shovel because its blade was longer (33 cm vs. 23 cm) and thicker than the standard shovel, which made it more difficult to insert into the substrate. McNeil samples required the longest collection time because substrate was excavated from the coring cylinder by hand and a time-consuming rinsing procedure was necessary to clean particles from the inside surfaces of the sampler.
Substrate armoring and composition also affected sample
collection time. The sampling crew indicated that the average sample collection
time was longer in Skookum Creek because large particles were encountered
more frequently. The presence of particles greater than 75 mm impeded sample
collection with all methods by obstructing the downward motion of the sampler,
however the McNeil sampler and the modified shovel with its longer blade
appeared to most affected. The sampling crew observed that greater body
weight, strength and experience of the sampling personnel increased the
speed and ease of sampling, particularly when inserting the McNeil sampler
or the modified shovel in substrate with large particles. In addition to
increasing the time to collect a sample, sampling sites occasionally were
abandoned in cases where the samplers could not be inserted. In 22 of 26
cases where sampling locations had to be abandoned, the dominant or subdominant
surface substrate was > 45 mm.
1. The standard shovel with stilling well can be an adequate substitute for the McNeil sampler when applied under conditions similar to those of the streams we sampled. There were no statistically significant differences in the mean percent fine sediment (< 0.85 mm) or geometric mean particle size between sample-pairs taken with the standard shovel with stilling well (S2) and the McNeil sampler. The percentage of fine sediment in S2 samples did not appear biased (either high or low) in comparison with McNeil samples and had similar precision to McNeil samples.
2. Statistically significant differences were detected in mean percent fine sediment and geometric mean particle size between McNeil samples and samples taken with both the standard shovel without stilling well (S1) and the modified shovel (S3) in Kennedy Creek. The percentage of fine sediments in S1 and S3 samples was biased (low) in comparison with McNeil samples in Kennedy Creek. Due to the large amount of variation, regressions were not useful for converting S1 and S3 measurements to equivalent McNeil sampler measurements for percent fine sediment. Consequently, the standard shovel (without stilling well) and the modified shovel are not adequate substitutes for the McNeil sampler under conditions similar to Kennedy Creek.
3. In five of six comparisons between McNeil and shovel-based sample pairs, the percentage of material in the smallest size category (particles < 0.106) was significantly different. In all cases, the average percent of particles < 0.106 was greater in McNeil samples than in shovel-based samples. This may be due to the plunger mechanism on the McNeil sampler, which captures water containing suspended sediments that is lost in shovel samples.
4. Differences in percent fine sediment between McNeil samples and paired samples for each shovel-based method could not be correlated with water depth or velocity. Nonetheless, we suspect these factors do influence the comparability of McNeil and shovel-based samples.
5. It appears that the presence and abundance of large particles influences the comparability of McNeil and shovel-based samples. There was a significant correlation between the difference in percent fine sediment between McNeil and shovel-based samples and the percentage of particles greater than 3.35 mm (in all cases) and GMPS (10 of 12 cases).
6. Samples collected with all three shovel-based sampling methods were approximately half the carry-out weight of McNeil samples. The smaller sample size and reduced water volume allow shovel-based samples to be transported in two gallon buckets. The reduced weight and bulk of shovel samples is advantageous when sampling sites are long distances from roads.
7. Collection time for the shovel-based sampling methods was substantially less than for the McNeil sampler. The standard shovel with stilling well (S2) averaged one-third the collection necessary for a McNeil sample (three minutes and nine minutes, respectively). The reduced time necessary to collect samples would be advantageous when numerous samples are required or when the time available to collect samples is limited.
8. There is no advantage gained in processing time for
samples collected with the shovel-based methods. Mean processing times
for all shovel-based methods ranged within 2.5 minutes of McNeil sample
processing times. Since the time required to process samples is much greater
than the time required to collect them, savings in sampling time will not
greatly affect the total time required to complete a gravel sampling program.
1. Mean differences in the percentage of fine sediment ranging from -0.7 to 1.0 % were observed between the McNeil sampler and the standard shovel with stilling well. However, since the power of our test inadequate to detect significant differences less than 3 %, we recommend limiting the use of the standard shovel with stilling well to situations where differences of 3 % in fine sediments will not affect data interpretation, such as initial habitat assessments.
2. We recommend continued use of the McNeil sampler in situations when a high degree of accuracy is important since other studies have shown that it provides the most accurate characterization of overall substrate composition (Young et al., 1991a).
3. In monitoring studies where detecting trends over time is important , we recommend using the same sampling method for follow-up monitoring as was used to establish the baseline. Changing methods during the course of a monitoring study would make it difficult to differentiate changes in spawning gravel composition from possible differences due to change in sampling methods.
4. We recommend additional testing of the difference in percent fine sediment between the McNeil sampler and the standard shovel with stilling well in additional stream segments representing a greater diversity of sampling conditions.
5. We recommend collection of a larger data set encompassing a greater range of water depths, velocity and substrate size to further investigate the effect of these factors on samples collected with various sampling methods.
6. We recommend investigation of the effect of volumetric
processing procedures on measurement of sediment < 0.1 mm.
Bjornn, T.C. 1968. Survival and emergence of trout and salmon in various gravel-sand mixtures. Pages 80-88 In: Proceedings of a forum on the relation between logging and salmon. Amer. Inst. Fisheries Research Biologists and Alaska Dept. Fish and Game. Juneau.
Cederholm, C.J., L.M. Reid, B.G. Edie and E.O Salo. 1982. Effects of forest road erosion on salmonid spawning gravel composition and populations of the Clearwater River, Washington. Pages 1-17 In: Hashagen, K.A. (ed.). Habitat disturbance and recovery; proceedings of a symposium. California Trout. San Francisco.
Church, M.A., D.G. McLean and J.F. Wolcott. 1987. River bed gravels: sampling and analysis. Pages 43- 79 In: C.R. Thorne, J.C. Bathurst and R.D. Hey (eds.). Sediment transport in gravel-bed rivers. John Wiley and Sons, Ltd.
Cohen, J. 1988. Statistical power analysis for the behavioral sciences. Lawrence Erlbaum Ass., Publishers. Hillsdale, New Jersey. 567 p.
Conover, W. J. 1980. Practical nonparametric statistics, second edition. John Wiley and Sons, New York. 493 p.
Draper, N. R. and H. Smith. 1981. Applied regression analysis. John Wiley and Sons, New York. 709 p.
Grost, R. T., W. A. Hubert, and T. A. Wesche. 1991. Field comparison of three devices used to sample substrate in small streams. N. Amer. J. Fish. Manage. 11:347-351.
Kleinbaum, D. G. and L. L. Kupper. 1978. Applied regression analysis and other multivariate methods. Duxbury Press, North Scituate, Massachusetts. 556 p.
McNeil, W.F. and W.H. Ahnell. 1964. Success of pink salmon spawning relative to size of spawning bed materials. USFWS Special Scientific Report- Fisheries No. 469. Washington, D.C.
Milliken, G. A. and D. E. Johnson. 1992. Analysis of messy data: designed experiments. Chapman and Hall, New York. 768 p.
Peterman, R.M. 1990. Statistical power analysis can improve fisheries research and management. Can. J. Fish. Aquat. Sci. 47:1-15.
Phillips, R.W., R.L. Lantz, E.W. Claire and J.R. Moring. 1975. Some effects of gravel mixtures on emergence of coho salmon and steelhead trout fry. Trans. Amer. Fish. Soc. 104(3):461-466.
Schuett-Hames, D., B. Conrad, M. McHenry, P. Peterson and A. Pleus. 1994. Salmonid spawning gravel composition module. In: D. Schuett-Hames, A. Pleus, L. Bullchild and S. Hall (eds.). Timber-Fish-Wildlife ambient monitoring manual. TFW-AM9-94-001. Northwest Indian Fisheries Commission. Olympia.
Scrivener, J.C. and M.J. Brownlee. 1989. Effects of forest harvesting on spawning gravel and incubation survival of chum (Oncorhynchus keta) and coho salmon (O. kisutch) in Carnation Creek, British Columbia. Can. J. Fish. Aquat. Sci. 46:681-696.
Tagart, J.V. 1976. The survival from egg deposition to emergence of coho salmon in the Clearwater River, Jefferson County, Washington. M.S. Thesis. University of Washington. Seattle.
Tripp, D. and V.A. Poulin. 1986. The effects of logging and mass wasting on salmonid spawning habitat in streams on the Queen Charlotte Islands. Land Management Report No. 50. B.C. Ministry of Forests and Lands. Vancouver, B.C.
Washington Forest Practices Board (WFPB). 1995. Washington Forest Practices Board Manual: standard methodology for conducting Watershed Analysis. Wash. Dept. Natural Resources. Forest Practices Division. Olympia.
Young, M. K., W. A. Hubert, and T. A. Wesche. 1990. Effect of substrate composition and stock origin on the survival to emergence of brown trout: a laboratory study. Northwest Science 64(4):224-231.
Young, M. K., W. A. Hubert, and T. A. Wesche. 1991a. Biases associated with four stream substrate samplers. Can. J. Fish. Aquat. Sci. 48:1882-1886.
Young, M. K., W. A. Hubert, and T. A. Wesche. 1991b. Selection
of measures of substrate composition to estimate survival to emergence
of salmonids and to detect changes in stream substrates. North American
Journal Fisheries Management 11:339-346.
Appendix Table 1. Summary statistics for the comparison of the paired McNeil sampler- shovel S1 samples collected from Kennedy Creek.
| Sieve | Mean Volume | Percent | McNeil > | ||
| Size (mm) | McNeil | Shovel S1 | Difference | Shovel S1a | Significanceb |
| 75.00 | - | - | - | - | - |
| 25.00 | 0.2657 | 0.2920 | -2.6% | 12/24 | 0.603 |
| 9.50 | 0.3157 | 0.3256 | -1.0% | 12/24 | 0.584 |
| 3.35 | 0.1532 | 0.1480 | 0.5% | 10/24 | 0.663 |
| 2.00 | 0.0466 | 0.0433 | 0.3% | 12/24 | 0.638 |
| 1.00 | 0.0458 | 0.0388 | 0.7% | 14/24 | 0.390 |
| 0.85 | 0.0105 | 0.0080 | 0.2% | 14/24 | 0.088 |
| 0.50 | 0.0374 | 0.0321 | 0.5% | 15/24 | 0.033 |
| 0.25 | 0.0640 | 0.0645 | 0.0% | 10/24 | 0.966 |
| 0.106 | 0.0247 | 0.0212 | 0.4% | 15/24 | 0.099 |
| <0.106 | 0.0364 | 0.0162 | 2.0% | 23/24 | 0.000 |
| Pooled | |||||
| ³3.35 | 0.7346 | 0.7759 | -4.1% | 6/24 | 0.005 |
| 0.85-2.00 | 0.1029 | 0.0901 | 1.3% | 14/24 | 0.452 |
| %Fines | 0.1625 | 0.1340 | 2.9% | 20/24 | 0.001 |
| GMPS | 11.206 | 13.662 | 21.9% | 8/24 | 0.030 |
b Significance levels 0.005 for the individual
sieve size categories and 0.05 for the pooled categories and for the geometric
mean particle size are considered significant. Significant tests are in
bold type.
Appendix Table 2. Summary statistics for the comparison of the paired McNeil sampler- shovel S2 samples collected from Kennedy Creek.
| Sieve | Mean Volume | Percent | McNeil > | ||
| Size (mm) | McNeil | Shovel S2 | Difference | Shovel S2a | Significanceb |
| 75.00 | - | - | - | - | - |
| 25.00 | 0.2533 | 0.2386 | 1.5% | 20/38 | 0.279 |
| 9.50 | 0.3294 | 0.3287 | 0.1% | 16/38 | 0.184 |
| 3.35 | 0.1634 | 0.1802 | -1.7% | 13/38 | 0.040 |
| 2.00 | 0.0441 | 0.0484 | -0.4% | 15/38 | 0.323 |
| 1.00 | 0.0410 | 0.0436 | -0.3% | 16/38 | 0.912 |
| 0.85 | 0.0102 | 0.0114 | -0.1% | 14/38 | 0.227 |
| 0.50 | 0.0336 | 0.0412 | -0.8% | 15/38 | 0.074 |
| 0.25 | 0.0606 | 0.0650 | -0.4% | 16/38 | 0.275 |
| 0.106 | 0.0246 | 0.0223 | 0.2% | 21/38 | 0.337 |
| <0.106 | 0.0378 | 0.0181 | 2.0% | 34/38 | 0.000 |
| Pooled | |||||
| ³3.35 | 0.7480 | 0.7501 | -0.2% | 16/38 | 0.464 |
| 0.85-2.00 | 0.0953 | 0.1034 | -0.8% | 15/38 | 0.509 |
| %Fines | 0.1566 | 0.1465 | 1.0% | 22/38 | 0.302 |
| GMPS | 11.640 | 11.522 | -1.0% | 18/38 | 0.819 |
b Significance levels 0.005 for the individual
sieve size categories and 0.05 for the pooled categories and for the geometric
mean particle size are considered significant. Significant tests are in
bold type.
Appendix Table 3. Summary statistics for the comparison of the paired McNeil sampler- shovel S3 samples collected from Kennedy Creek.
| Sieve | Mean Volume | Percent | McNeil > | ||
| Size (mm) | McNeil | Shovel S3 | Difference | Shovel S3a | Significanceb |
| 75.00 | - | - | - | - | - |
| 25.00 | 0.2444 | 0.2743 | -3.0% | 13/24 | 0.331 |
| 9.50 | 0.3110 | 0.3174 | -0.6% | 10/24 | 0.418 |
| 3.35 | 0.1622 | 0.1775 | -1.5% | 11/24 | 0.293 |
| 2.00 | 0.0500 | 0.0505 | -0.1% | 14/24 | 0.983 |
| 1.00 | 0.0488 | 0.0481 | 0.1% | 9/24 | 0.648 |
| 0.85 | 0.0112 | 0.0102 | 0.1% | 15/24 | 0.550 |
| 0.50 | 0.0395 | 0.0375 | 0.2% | 11/24 | 0.763 |
| 0.25 | 0.0644 | 0.0551 | 0.9% | 16/24 | 0.027 |
| 0.106 | 0.0231 | 0.0160 | 0.7% | 21/24 | 0.000 |
| <0.106 | 0.0421 | 0.0133 | 2.9% | 24/24 | 0.000 |
| Pooled | |||||
| ³3.35 | 0.7208 | 0.7692 | -4.8% | 6/24 | 0.002 |
| 0.85-2.00 | 0.1101 | 0.1088 | 0.1% | 14/24 | 0.877 |
| %Fines | 0.1692 | 0.1220 | 4.7% | 19/24 | 0.000 |
| GMPS | 10.872 | 12.915 | 18.8% | 7/24 | 0.023 |
b Significance levels 0.005 for the individual
sieve size categories and 0.05 for the pooled categories and for the geometric
mean particle size are considered significant. Significant tests are in
bold type.
Appendix Table 4. Summary statistics for the comparison of the paired McNeil sampler- shovel S1 samples collected from Skookum Creek.
| Sieve | Mean Volume | Percent | McNeil > | ||
| Size (mm) | McNeil | Shovel S1 | Difference | Shovel S1a | Significanceb |
| 75.00 | 0.0110 | 0.0621 | -5.1% | 1/24 | 0.012 |
| 25.00 | 0.2524 | 0.2321 | 2.0% | 13/24 | 0.320 |
| 9.50 | 0.2122 | 0.2015 | 1.1% | 13/24 | 0.208 |
| 3.35 | 0.1842 | 0.1659 | 1.8% | 16/24 | 0.023 |
| 2.00 | 0.0741 | 0.0640 | 1.0% | 17/24 | 0.003 |
| 1.00 | 0.0813 | 0.0775 | 0.4% | 12/24 | 0.473 |
| 0.85 | 0.0194 | 0.0204 | -0.1% | 11/24 | 0.589 |
| 0.50 | 0.0619 | 0.0668 | -0.5% | 10/24 | 0.317 |
| 0.25 | 0.0651 | 0.0722 | -0.7% | 9/24 | 0.267 |
| 0.106 | 0.0187 | 0.0217 | -0.3% | 10/24 | 0.226 |
| <0.106 | 0.0197 | 0.0158 | 0.4% | 21/24 | 0.000 |
| Pooled | |||||
| ³3.35 | 0.6598 | 0.6616 | -0.2% | 12/24 | 0.541 |
| 0.85-2.00 | 0.1748 | 0.1620 | 1.3% | 14/24 | 0.089 |
| %Fines | 0.1654 | 0.1765 | -1.1% | 12/24 | 0.546 |
| GMPS | 9.169 | 10.787 | 17.6% | 9/24 | 0.197 |
b Significance levels 0.00455 for the individual
sieve size categories and 0.05 for the pooled categories and for the geometric
mean particle size are considered significant. Significant tests are in
bold type.
Appendix Table 5. Summary statistics for the comparison of the paired McNeil sampler- shovel S2 samples collected from Skookum Creek.
| Sieve | Mean Volume | Percent | McNeil > | ||
| Size (mm) | McNeil | Shovel S2 | Difference | Shovel S2a | Significanceb |
| 75.00 | 0.0192 | 0.0450 | -2.6% | 3/24 | 0.164 |
| 25.00 | 0.2535 | 0.2656 | -1.2% | 10/24 | 0.452 |
| 9.50 | 0.2280 | 0.2007 | 2.7% | 20/24 | 0.006 |
| 3.35 | 0.1782 | 0.1631 | 1.5% | 17/24 | 0.079 |
| 2.00 | 0.0699 | 0.0652 | 0.5% | 16/24 | 0.241 |
| 1.00 | 0.0744 | 0.0761 | -0.2% | 10/24 | 0.922 |
| 0.85 | 0.0167 | 0.0178 | -0.1% | 8/24 | 0.478 |
| 0.50 | 0.0558 | 0.0605 | -0.5% | 10/24 | 0.331 |
| 0.25 | 0.0625 | 0.0677 | -0.5% | 10/24 | 0.119 |
| 0.106 | 0.0199 | 0.0222 | -0.2% | 7/24 | 0.052 |
| <0.106 | 0.0218 | 0.0160 | 0.6% | 21/24 | 0.001 |
| Pooled | |||||
| ³3.35 | 0.6790 | 0.6744 | 0.5% | 10/24 | 0.944 |
| 0.85-2.00 | 0.1610 | 0.1592 | 0.2% | 13/24 | 0.877 |
| %Fines | 0.1600 | 0.1665 | -0.6% | 10/24 | 0.570 |
| GMPS | 9.740 | 10.899 | 11.9% | 8/24 | 0.422 |
b Significance levels 0.00455 for the individual
sieve size categories and 0.05 for the pooled categories and for the geometric
mean particle size are considered significant. Significant tests are in
bold type.
Appendix Table 6. Summary statistics for the comparison of the paired McNeil sampler- shovel S3 samples collected from Skookum Creek
| Sieve | Mean Volume | Percent | McNeil > | ||
| Size (mm) | McNeil | Shovel S3 | Difference | Shovel S3a | Significanceb |
| 75.00 | 0.0274 | 0.0394 | -1.2% | 4/31 | 0.358 |
| 25.00 | 0.2375 | 0.2523 | -1.5% | 12/31 | 0.349 |
| 9.50 | 0.2233 | 0.2085 | 1.5% | 20/31 | 0.080 |
| 3.35 | 0.1811 | 0.1636 | 1.7% | 19/31 | 0.034 |
| 2.00 | 0.0655 | 0.0611 | 0.4% | 19/31 | 0.238 |
| 1.00 | 0.0708 | 0.0670 | 0.4% | 19/31 | 0.256 |
| 0.85 | 0.0180 | 0.0177 | 0.0% | 18/31 | 0.632 |
| 0.50 | 0.0636 | 0.0665 | -0.3% | 14/31 | 0.950 |
| 0.25 | 0.0716 | 0.0824 | -1.1% | 11/31 | 0.067 |
| 0.106 | 0.0200 | 0.0224 | -0.2% | 11/31 | 0.027 |
| <0.106 | 0.0212 | 0.0191 | 0.2% | 21/31 | 0.035 |
| Pooled | |||||
| ³3.35 | 0.6692 | 0.6638 | 0.5% | 15/31 | 0.977 |
| 0.85-2.00 | 0.1543 | 0.1457 | 0.9% | 21/31 | 0.211 |
| %Fines | 0.1765 | 0.1904 | -1.4% | 15/31 | 0.533 |
| GMPS | 9.600 | 10.496 | 9.3% | 14/31 | 0.308 |
b Significance levels 0.00455 for the individual
sieve size categories and 0.05 for the pooled categories and for the geometric
mean particle size are considered significant. Significant tests are in
bold type.
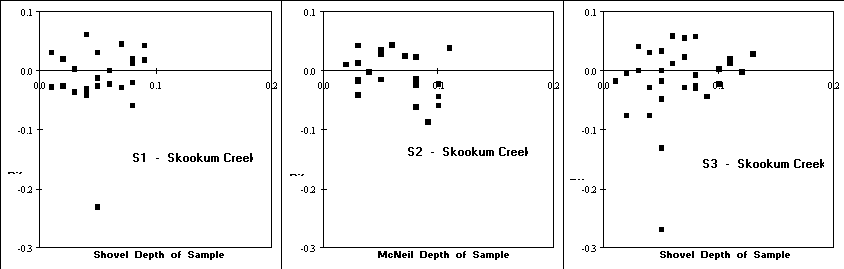
Figure 6. Plots of depth of sample versus difference in %Fines between the paired samples for the McNeil and the three shovel-based methods for samples collected at Kennedy Creek and Skookum Creek.
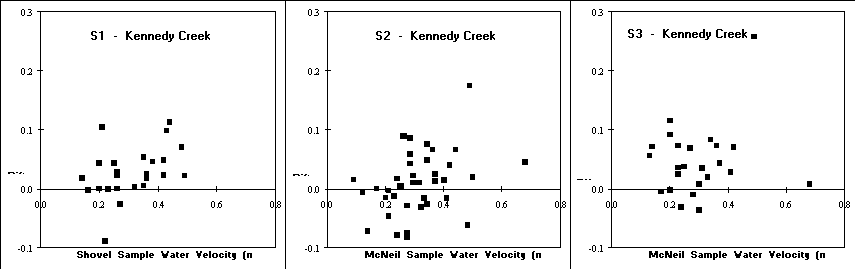
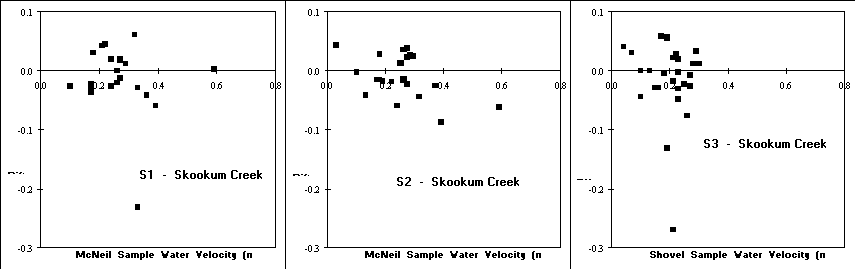
Figure 7. Plots of water velocity versus difference in %Fines between the paired samples for the McNeil and the three shovel-based methods for samples collected at Kennedy Creek and Skookum Creek.
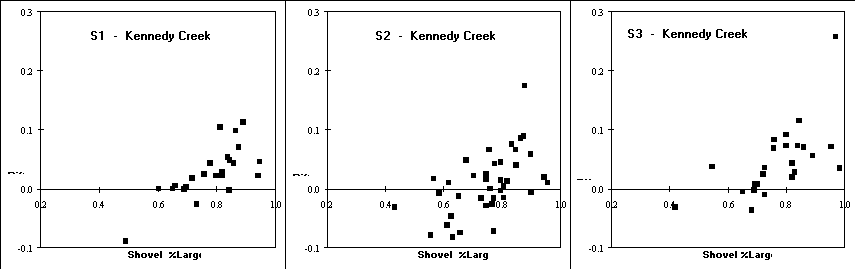
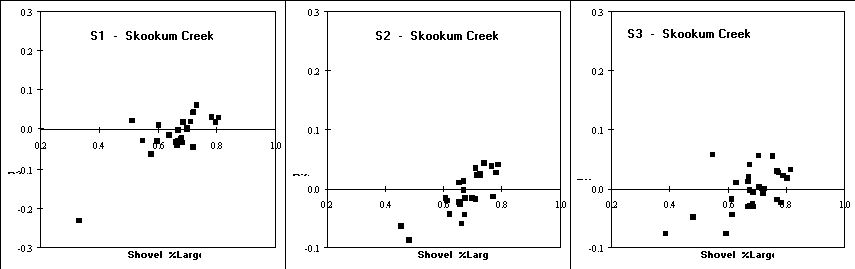
Figure 8. Plots of %Large versus difference in %Fines
between the paired samples for the McNeil and the three shovel-based methods
for samples collected at Kennedy Creek and Skookum Creek.